MQL Data Types

MQL4 supports seven data types within the program. Each type is associated with different trading tasks that programmers need to perform. The goal of this article is to provide a brief reference for when to use each data type.

The double data type is probably the most common type found in MQL programs. This is because it is the type responsible for calculating floating point numbers. Say for example, that an expert advisor needs to determine when to adjust a trailing stop. The expert advisor looks at the current price and subtracts it from the current stop loss to maintain the appropriate distance (1.3230-1.3209=0.0021). The distance requires a decimal point. When the expert advisor saves the distance to memory, it needs to save the information after the decimal point. That forces the programmer to choose a variable of type double.

Integers, or int, is the simpler version of double. Double values require a decimal place to hold the number's value accurately. An integer, or whole number, does not have a decimal place. Integers are appropriately used when the MQL programmer knows for a certain fact that the number will never contain a decimal. An example would be if you wanted to implement a max trades feature. If the number of open trades in the account exceeds a certain number, then prevent trades. We know in advance that there is no such thing at 4.76 trades being open. There can only be 4 trades open or 5 trades open. This clearly indicates the need to use an integer.

Datetime values are just what they sound like. They represent both the date and time. More specifically, a datetime variable represents the number of seconds that have elapsed since January 1, 1970. This is where it gets a little tricky. The number of seconds that have elapsed is actually an integer. Datetimes store integer values but then associate them with a date and time.

A value of 0 would indicate that the time is 00:00 on January 1, 1970. A value of 60 stands for one minute later at 00:01 1/1/1970, and so on. One benefit of knowing that the datetime type stores information as integers is that you can easily determine the amount of time that happens between an event. If the event starts at 15:35 and ends at 18:12, you can simply subtract 18:12 - 15:35 and wind up with the number of seconds between those values. That information can then be used to determine the number minutes/hours/days between the two events.

The color data type, not surprisingly, holds color information such as black, yellow, red and so on. Much like datetime types, color also uses integers to store the information. The difference, though, is that extracting the color information from the integer is not at all obvious. Increasing a color type from 32768 by one will not necessarily make it more or less green. Colors use the integer information to retrieve the red, green and blue components of the color in hexadecimal format. Explaining hexadecimals is well beyond the scope of this article. It's unlikely to come up in your MQL programming. I've been doing this for over five years and only came across one project that required manipulating a color in way more complicated than alternating between two set colors.

A string is anything that resembles a word or sentence. It always uses quotes to contain the information. My favorite use of strings is to gather information to display on the chart or in a log file whenever I need to debug an expert advisor.

Char is the final data type. It's so closely related to a string that I wasn't even aware this type existed until I looked up information for this article. If we study the word "trade", then we will find that it is composed of the five characters t, r, a, d and e.

A final note on data types. There are two ways that types are held in memory. An extern variable is one that shows up in the inputs screen whenever an expert advisor or indicator loads. Static variables are the opposite. They remain within the MQL program and never visible outside of it.

Recall that Martingale systems aim to never lose money. Instead of accepting losses and moving on, a Martingale betting strategy doubles the previous bet. Whenever a win finally does happen, all losses up until that point are regained. The trade also gains the same amount of profit that the original trade hoped to capture.

Trading forex with a Martingale money management system will almost inevitably lead to blowing up an account. I've written about this inevitable outcome repeatedly over the past six months. At the risk of beating a dead horse, I figured that visual proof would relieve any lingering hopes once and for all.

The goal of the exercise is to focus on the risk of ruin rather than the profits acquired. As time goes on, the likelihood of ruin goes up with the number of trades placed. A trade is each time a new transaction enters. It does not matter whether or not the last trade was a winner or a loser.

Fifty trades on most Martingale systems corresponds to anything from several days to several weeks. The level of aggression used in the trade level (i.e., the pip distance used to open a new trade) is what most strongly affects the amount of time required to reach fifty trades.

Placing 50 trades shows what most traders know. The returns look fairly nice at that point. A return of 20% on the account shows a 40% probability of occurring. The risk of wiping out the account looks meek at 8.5%.

Increasing the number of trades to 200, which corresponds to several weeks or months, the odds of outright failure skyrocket to 35%. The lucky traders that have not yet blown up show returns ranging from 20% all the way to 300%. The total risk is more apparent, although many traders fall victim to the lure of quick, large returns. If it all looks too easy at this point in time, that's because it is.

Going out to 1,000 trades, which I roughly ballpark as the amount of trades an average expert advisor might complete in 9 months to a year, is where the inevitable result is obvious. The odds of reaching a zero balance reach 95%. A tiny handful of traders are floating huge returns. As the number of trades increases from 1,000 to 2,000 to 10,000, the tiny fraction of accounts left eventually dwindles down to zero.

The test assumes that the trader uses fixed fractional money management set at 1% of the account value. Recall from earlier experiments that a 1% risk value will almost never ruin an account after 200 trades. The percent accuracy for the trades remains at 50%, which is perfectly random. The random number file has been upgraded to include 10 million random numbers instead of the previous half a million.

Fiber projects compete for transatlantic speed

A few weeks ago I wrote about Project Express, a new fiber-optic cable being built across the Atlantic that will give a select number of high-frequency traders a tiny speed advantage in trading times between New York and London. Currently, data take 64 milliseconds (give or take a few fractions of an eye blink) to travel round-trip between New York and London along a cable built in 1998 called the AC-1.


http://www.businessweek.com/articles/2012-04-23/high-speed-trading-my-laser-is-faster-than-your-laser

http://www.businessweek.com/articles/2012-03-29/trading-at-the-speed-of-light

In April, the Canadian research ship Coriolis II will set out from Halifax to survey parts of the continental shelf stretching 1,000 miles off the east coast of Nova Scotia.

The ship has been hired by Hibernia Atlantic, a Summit, New Jersey-based company that operates undersea telecom cables, to map out a new $300 million trans-Atlantic fiber-optic line called Project Express. The cable will stretch 3,000 miles beneath the North Atlantic, connecting financial markets in London and New York at record transmission speeds. A small group of U.S. and European high-speed trading firms will pay steep fees to use the cable.

http://www.bloomberg.com/news/2012-03-29/cable-across-atlantic-aims-to-save-traders-milliseconds.html

Fixed Fractional Money Management

Trading totally at random with a 50% winning percentage and an R multiple of 1 yields no advantage, as I discussed last week in modeling money management. Remember that an R multiple is the average win to the average loss. Such a system poses neither an advantage or disadvantage. The average outcome should come out extremely close to the starting balance.

Most traders focus on risking a set dollar amount such as $1,000 on a given trade. Fixed fractional money management updates that dollar figure after every single trade. It changes the overall outcome after you add up all the winners and all of the losers. Remember that trading is the net outcome of several hundred trades or even thousands of trades. The power of money management comes into play as the number of trades increases.

Fixed fractional money management stretches some portions of the bell curve and compresses other regions. Before we get into that, it's important to remember what fixed fractional money management means. It stands for the idea of risking a set percentage of the current account equity rather than the starting equity.

Consider an example where the account balance starts at $100,000 risking 1%. Both methods risk the same amount on the first trade, $1,000. The next trade, however, will yield a different risk amount. A win on the previous trade would increase the account equity to $101,000. One percent of a 101 grand is $1,010 of risk on the next trade. A whopping ten dollar change.

That may seem trivial. It is most certainly not over the long run.

Examples

Consider a trader that plays the coin toss game and has a system with the following characteristics:

He starts with a $100, 000 account balance
His R multiple is 1.0
He wins 50% of the time with no trading costs
He risks 1%

The absolute worst outcome of playing the coin toss with a fixed dollar risk of $1,000 is a loss of $46,000. Adding fixed fractional money management during that difficult drawdown improves the drawdown to a less substantial loss of $37,500. The worst drawdown goes from -46% to -37.5%. The method drags the absolute worst case scenario and pulls it closer to the average. When an unlucky, devastating drawdown kicks in, the technique reduces the losses that the trader experiences.

The best case scenario for fixed dollar risk is a $58,000 (58%) return. Adding money management to the system dramatically stretches the best case scenario further to the right. It improves to a $76,000 return (76%). The good times get a lot better without changing anything at all about the trading system. The method stretches positive returns away from the average. The trader walks away with more money in his pocket.

The natural instinct is to conclude that fixed fractional money management is the way to go. I agree. It improves the risk reward profile of a totally random strategy. Adding it to a real trading system should help control parameters that most traders consider critical like drawdowns and maximizing the return.

An important consequence of using fixed fractional money management, however, is that the odds of receiving a below average return increase somewhat. The coin toss game suffered a below average return 47% of the time. Applying fixed fractional money management increased the likelihood of a below average return to 53%. The effect is not all that much. Losing is more likely. But when it happens, the "loss" is so negligible that it can be thought of as breaking even.

Random numbers occasionally follow a seemingly non-random pattern such as loss-win-loss-win. When this occurs, the size of the trade on the losses is bigger than the trade size of the winners. Even if the winning percentage comes out at precisely 50%, those wins get slightly overshadowed by the losers. That micro effect of slightly larger losses than gains shows up as a slightly increased risk of not making as much money as expected.

Graphing all outcomes



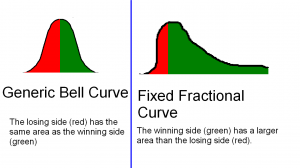
Red areas represent the losing outcomes while green areas represent the winners. Money management is really about maximizing the ratio of green area to red area. Random trades with no expectation of profit yield a bell curve, which appears on the left.

Fixed fractional moves the highest density of returns slightly to the left. Doing so creates the trivial disadvantage of a slightly increased risk of negligible loss. Importantly, the far left side (the worst case loser) gets dragged much closer to the average. The far right side (the best case winner), gets stretched much further from the average. The goal is to make the green area larger than the red area to where we actually expect a profit.

JPM accidentally moves markets

Market-moving trades by JPMorgan Chase & Co. (JPM) (JPM)’s chief investment office probably will force regulators to seek more detail on banks’ derivatives positions to help them distinguish risk management from speculation.

Bruno Iksil, a London-based trader in the unit, has built derivatives positions linked to corporate credit that are so big he’s moved markets, according to hedge fund managers and dealers. While Joe Evangelisti, a bank spokesman, said yesterday that the trades are part of the firm’s hedging strategy, four market participants said they resemble proprietary bets, or wagers with the lender’s own money.

http://www.businessweek.com/news/2012-04-09/jpmorgan-s-iksil-seen-spurring-regulators-to-dissect-trading

Money Management Modeling

We recently developed software to model the affects of random chance on money management. Although computers are capable of producing pseudo-random numbers, the pseudo-random procedure introduces bias into the random distribution.

We determined to source our random numbers from random.org. The web site obtains purely random streams of bits taken from atmospheric noise. We then use binary mathematics to change those bits into numbers ranging from 1-10,000. Say, for example, that we want to model a trading system with a winning percentage of 50%. Whenever a number comes out between 1-5,000, we consider that a winner. Anything above 5,000 marks a loser.

Modifying the winning percentage to 65% works the same way. Any number less than 6,500 represents a winning trade. Numbers above 6,500 signal a loss. The modeling quality is accurate to the thousandth decimal place. That type of accuracy is way more accurate than the "known" accuracy of your trading system, which can only be known within a few whole percentage points.

Most traders fall into the trap of thinking about their trades as individual outcomes. The more necessary way to view returns is as the sum of all individual outcomes. Losing on any given trade does not matter. It only matters whether the sum of all your winners is greater than all of the losers.

It gets more complicated, unfortunately. A system with 50% wins and a 1:1 payout will almost never come out at exactly breakeven. The mathematical expectation is that we expect to see a degree of drift in the returns solely due to random chance. I suggest reading more in the random trade outcomes and dollar profits section to get a better understanding of drift.

Lastly, we must delimit a sampling period for evaluating the final result. I arbitrarily set the default value to 200. That means that the software tells us the range of outcomes after 200 total trades. That may take more than a year for some traders. Daytraders may reach that benchmark in several weeks of trading. The question that we are answering is "what is my account balance likely to be after placing 200 trades?"

Coin Toss Trading Experiment

The first experiment is to analyze how dollar returns vary with a coin toss game and the most basic money management method. A starting balance of $100,000 is used with a risk of 1%. The risk will not change as in the fixed fractional method. Instead, we will leave the lots fixed in order to strictly understand random chance. Wins always earn $1,000. Losses always lose $1,000. The odds of a coin toss are 50% wins with 50% losses and a 1:1 reward risk ratio.

The average trade comes out to $99,868.36, almost exactly $100,000. It's what we expect for a 50-50 game with a 1:1 reward risk ratio. What I find interesting is the standard deviation of $14,377 and how it changes. I don't want to cover scary math topics. The layman's explanation is that the standard deviation is the "normal" range from the average that you might expect. The $100,000 balance, in most cases, would either lose $14,000 or make $14,000.

Everything beyond those standard deviation boundaries represent the less likely wild scenarios. The minimum outcome comes out to $58,o00, a massive 42% loss. This had a 0.54% chance of occuring. The maximum outcome shows as $158,000, a monster 58% return. This had an even smaller chance of occurring, only 0.1% (1 in every 1,000 trials).

Changing the account risk dramatically affects the standard deviation. 1% strikes most traders as sane and reasonable. Yet, there is a small chance of losing half the account to drawdown strictly because of terrible luck. Decreasing the overall risk by a fourth to 0.25% drops the standard deviation by exactly one fourth. The worst case scenario shrinks to a highly tolerable $11,500 drawdown (11.5%). Most traders would find a number between 10%-20% reasonable. The consequence of the reduced risk is that the best case scenario drops correspondingly down to a 14.5% gain.

Stretching the risk out to 2%, a normal industry practice, turns out to be risking accounting suicide with the coin toss game. The worst case scenario drops the final account balance down to $8,000, a staggering 92% loss.

The goal is to help you define risk from a gut feeling matter into something more tangible and calculated. Too many traders enter the market day dreaming about profits. Risk enters the picture, but too few traders actually understand the relationship between risk and reward. Hopefully, the picture of best, worst and average scenarios is starting to become more clear for you.

Forticlient Lite Internet Security

FortiClient Lite is a free endpoint protection suite that includes malware/virus detection, parental web control, and VPN. Malware is detected using updated threat intelligence and definitions from Fortinet's FortiGuard Labs. Parental control offers a simple and effective way to block malicious and explicit web sites. Single VPN configuration allows quick and easy secure, remote access via IPSec or SSL protocols. FortiClient Lite leverages FortiClient's Antivirus technology, developed in-house by Fortinet. FortiClient Antivirus has achieved more than twenty VB100 awards and is capable of detecting threats on both a reactive and proactive basis. Proactive detection is based on detecting zero-day malware that has never been seen before in the wild. 

http://www.forticlient.com/lite.html

Contact EES for Forticlient Premium or other Fortinet products such as firewalls.